吴恩达机器学习一站式学习系列（4）——多变量线性回归(Linear Regression with Multiple Variables)

作者： /

多维特征Multiple Features

之前课程仅针对单一变量/特征进行回归，但现实中单一变量/调整很少，往往都会存在较多的特征。

多维特征是指在数据分析、机器学习和统计学等领域中，用于描述和表示数据的多个属性、变量或特征。每个特征可以看作是数据的一个维度，多个特征共同构成了数据的多维空间。多维特征用于捕捉数据的多方面信息，从而更全面地描述数据。

对房价模型增加更多的特征，例如房间数楼层等，构成一个含有多个变量的模型，模型中的特征为多个数值。

多维梯度下降Gradient Descent for Multiple Variables

与单变量线性回归类似，在多变量线性回归中，也需要构建一个代价函数。同理，代价函数是所有建模误差的平方和，目的要找出使得代价函数最小的一系列参数。

代价函数

梯度下降

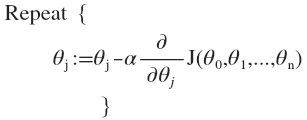
所以经过推导等运算，得出下图结果；开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。

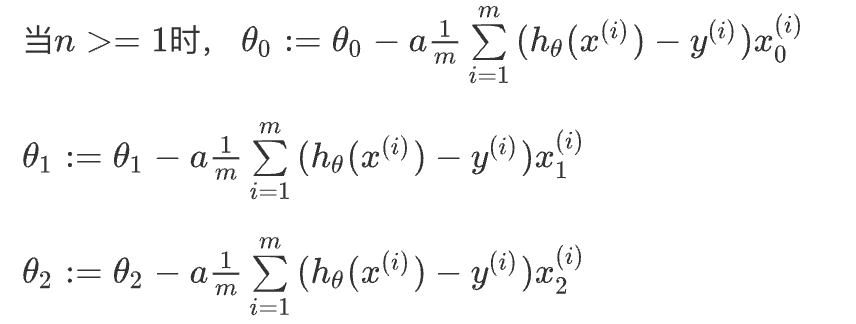
Python代码

def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

梯度下降法实践——特征缩放Feature Scaling

特征缩放是在数据预处理过程中的一个重要步骤，旨在将数据特征的值范围调整到合适的尺度，以便在机器学习算法中获得更好的性能。不同特征可能具有不同的尺度和分布，如果不进行特征缩放，某些机器学习算法可能会因为特征之间的差异而表现不佳。以下是常见的特征缩放方法：

  1. 标准化（Z-score 标准化）： 标准化是通过将每个特征的值减去其均值，然后除以标准差，从而使得特征的值具有均值为0，标准差为1的标准正态分布。这种方法适用于特征呈正态分布或近似正态分布的情况。
  2. 最小-最大缩放（Min-Max Scaling）： 最小-最大缩放通过对每个特征的值进行线性变换，将特征的值范围映射到一个指定的区间，通常是[0, 1]。这有助于消除特征之间的尺度差异，适用于有界的特征值情况。
  3. 归一化： 归一化是将特征的值映射到单位范数（向量的长度为1），通常使用L2范数进行缩放。这在需要对特征向量的幅度进行控制时很有用。
  4. Robust 缩放： 这种缩放方法对特征值的缩放不受极端值的影响。它通过减去特征值的中位数，然后除以四分位距来进行缩放。
  5. Log 缩放： 如果某个特征的分布呈现指数形式，可以考虑对其取对数，以使其更加符合线性关系。

为什么要进行缩放

让多维特征具有相近的尺度或者说在同一数量级上，这将帮助梯度下降算法更快地收敛。

以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-2000平方英尺，而房间数量的值则是0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图能，看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

解决方案

将所有特征的尺度都尽量缩放到-1到1之间。

梯度下降法实践——学习率Learning Rate

梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，不能提前预知，可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

梯度下降算法的每次迭代受到学习率的影响，如果学习率α过小，则达到收敛所需的迭代次数会非常高；如果学习率α过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。

通常可以考虑尝试些学习率：α=0.01,0.03,0.1,0.3,1,3,10… ；整体基本按照三倍进行尝试验证，去寻找大致的取值范围。

特征和多项式回归Features and Polynomial Regression

上文中提到的代价函数，最终的绘制基本都是一条直线；但其实现实中可能并非全部都是直线来拟合所有数据。

多项式回归（Polynomial Regression）是一种回归分析方法，用于建立自变量（特征）与因变量之间的关系，但与线性回归不同，它允许使用多项式函数来拟合数据，从而更好地适应非线性关系。

在线性回归中，我们假设自变量和因变量之间的关系是线性的，即可以用直线来表示。但在实际情况中，很多关系是非线性的，此时就可以考虑使用多项式回归。多项式回归通过引入高次项来建模非线性关系，其模型形式为：

如房价预测问题，有宽度和深度（长度）为两个参数/变量。

使用多项式回归可以更好地拟合一些曲线形状的数据。然而，需要注意以下几点：

  1. 阶数选择： 高阶多项式可以更好地拟合数据，但过高的阶数可能导致过拟合，使模型在训练数据上表现很好，但在新数据上表现较差。阶数的选择需要在模型复杂度和泛化能力之间进行平衡。
  2. 特征工程： 在使用多项式回归之前，有时需要对数据进行特征工程，如标准化、归一化、处理缺失值等，以确保模型的性能。
  3. 交叉验证： 使用交叉验证来评估模型的性能，特别是在选择多项式阶数时，可以通过交叉验证来找到最佳的阶数。
  4. 局限性： 多项式回归虽然可以拟合复杂的数据关系，但对于过于复杂的数据关系，也可能会导致过拟合问题。在某些情况下，其他非线性回归方法如岭回归、Lasso回归、核回归等可能更为适用。

正规方程Normal Equation

正规方程（Normal Equation）是一种用于解决线性回归问题的方法，它通过解析求解来找到最佳的回归系数，从而建立自变量与因变量之间的线性关系。通过正规方程，可以直接得到模型的参数，而无需迭代或优化过程。

xxxxxxxxxx
import numpy as np
    
 def normalEqn(X, y):
    
   theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X等价于X.T.dot(X)
    
   return theta

梯度下降与正规方程的比较

梯度下降正规方程
需要选择学习率不需要
需要多次迭代一次运算得出
当特征数量大时也能较好适用需要计算 如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为，通常来说当小于10000 时还是可以接受的
适用于各种类型的模型只适用于线性模型，不适合逻辑回归模型等其他模型

正规方程的优点包括：

  • 解析解： 可以直接从数学公式中求解，不需要迭代过程，计算结果直观。
  • 精确性： 当数据满足线性回归的基本假设时，正规方程可以得到精确的最优解。

正规方程也有一些限制和注意事项：

  • 计算复杂度： 在特征数很大时，计算 (X^T*X)^−1 的逆矩阵的计算复杂度较高，可能会导致计算开销很大。
  • 特征相关性： 如果自变量之间存在高度相关性，(X^T*X)^−1 的逆可能不存在或不稳定。
  • 计算资源： 对于大规模数据集，正规方程可能会消耗大量的计算资源和内存。

总结一下，只要特征变量的数目并不大，标准方程是一个很好的计算参数的替代方法。具体地说，只要特征变量数量小于一万，通常使用标准方程法，而不使用梯度下降法。

相关文章

滚动至顶部